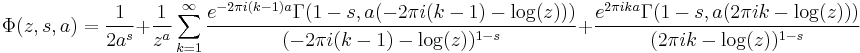Lerch zeta function
In mathematics, the Lerch zeta-function, sometimes called the Hurwitz–Lerch zeta-function, is a special function that generalizes the Hurwitz zeta-function and the polylogarithm. It is named after Mathias Lerch [1].
Contents |
Definition
The Lerch zeta-function is given by
A related function, the Lerch transcendent, is given by
The two are related, as
Integral representations
An integral representation is given by
for
A contour integral representation is given by
for
where the contour must not enclose any of the points 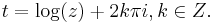
A Hermite-like integral representation is given by
for
and
for
Special cases
The Hurwitz zeta-function is a special case, given by
The polylogarithm is a special case of the Lerch Zeta, given by
The Legendre chi function is a special case, given by
The Riemann zeta-function is given by
The Dirichlet eta-function is given by
Identities
For λ rational, the summand is a root of unity, and thus 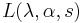 may be expressed as a finite sum over the Hurwitz zeta-function.
may be expressed as a finite sum over the Hurwitz zeta-function.
Various identities include:
and
and
Series representations
A series representation for the Lerch transcendent is given by
The series is valid for all s, and for complex z with Re(z)<1/2. Note a general resemblance to a similar series representation for the Hurwitz zeta function.
A Taylor's series in the first parameter was given by Erdélyi. It may be written as the following series, which is valid for
- (the correctness of this formula is disputed, please see the talk page)
Please see: B. R. Johnson, Generalized Lerch zeta-function. Pacific J. Math. 53, no. 1 (1974), 189–193. http://projecteuclid.org/Dienst/UI/1.0/Display/euclid.pjm/1102911791?abstract=
If s is a positive integer, then
A Taylor series in the third variable is given by
Series at a = -n is given by
A special case for n = 0 has the following series
An asymptotic series for 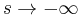
for 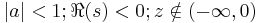 and
and
for 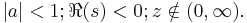
An asymptotic series in the incomplete Gamma function
for 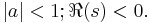
References
- Apostol, T. M. (2010), "Lerch's Transcendent", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR2723248, http://dlmf.nist.gov/25.14.
- Bateman, H.; Erdélyi, A. (1953), Higher Transcendental Functions, Vol. I, New York: McGraw-Hill, http://apps.nrbook.com/bateman/Vol1.pdf. (See § 1.11, "The function Ψ(z,s,v)", p. 27)
- Gradshteyn, I.S.; Ryzhik, I.M. (1980), Tables of Integrals, Series, and Products (4th ed.), New York: Academic Press, ISBN 0-12-294760-6. (see Chapter 9.55)
- Guillera, Jesus; Sondow, Jonathan (2008), "Double integrals and infinite products for some classical constants via analytic continuations of Lerch's transcendent", The Ramanujan Journal 16 (3): 247–270, arXiv:math.NT/0506319, doi:10.1007/s11139-007-9102-0, MR2429900. (Includes various basic identities in the introduction.)
- Jackson, M. (1950), "On Lerch's transcendent and the basic bilateral hypergeometric series 2ψ2", J. London Math. Soc. 25 (3): 189–196, doi:10.1112/jlms/s1-25.3.189, MR0036882.
- Laurinčikas, Antanas; Garunkštis, Ramūnas (2002), The Lerch zeta-function, Dordrecht: Kluwer Academic Publishers, ISBN 9781402010149, MR1979048.
- Lerch, Mathias (1887), "Note sur la fonction
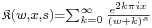 " (in French), Acta Mathematica 11 (1–4): 19–24, doi:10.1007/BF02612318, MR1554747.
" (in French), Acta Mathematica 11 (1–4): 19–24, doi:10.1007/BF02612318, MR1554747.
External links
- Aksenov, Sergej V.; Jentschura, Ulrich D. (2002), C and Mathematica Programs for Calculation of Lerch's Transcendent, http://aksenov.freeshell.org/lerchphi.html.
- Ramunas Garunkstis, Home Page (2005) (Provides numerous references and preprints.)
- Ramunas Garunkstis, Approximation of the Lerch Zeta Function (PDF)
- S. Kanemitsu, Y. Tanigawa and H. Tsukada, A generalization of Bochner's formula, (undated, 2005 or earlier)
- Weisstein, Eric W., "Lerch Transcendent" from MathWorld.
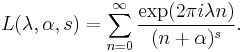
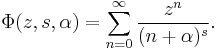
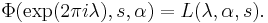
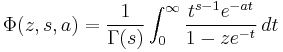
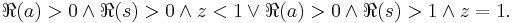
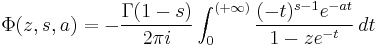
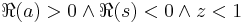
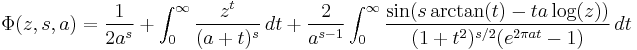
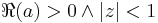
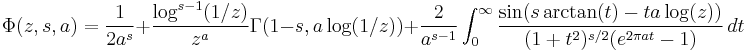
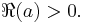
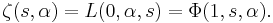
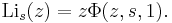
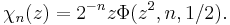
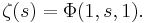
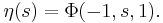
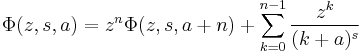
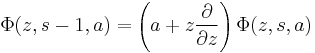
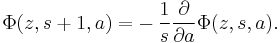
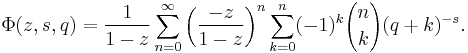
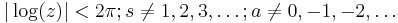
![\Phi(z,s,a)=z^{-a}\left[\Gamma(1-s)\left(-\log (z)\right)^{s-1}
%2B\sum_{k=0}^\infty \zeta(s-k,a)\frac{\log^k (z)}{k!}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/c548856f14546af8f73ee01e6cbb42d5.png)
![\Phi(z,n,a)=z^{-a}\left\{
\sum_{{k=0}\atop k\neq n-1}^ \infty \zeta(n-k,a)\frac{\log^k (z)}{k!}
%2B\left[\Psi(n)-\Psi(a)-\log(-\log(z))\right]\frac{\log^{n-1}(z)}{(n-1)!}\right\}.](/2012-wikipedia_en_all_nopic_01_2012/I/6a88947b0f03288fd97fdd91adf19af2.png)
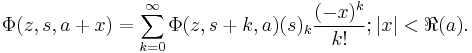
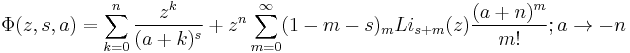
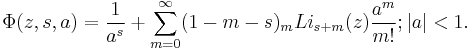
![\Phi(z,s,a)=z^{-a}\Gamma(1-s)\sum_{k=-\infty}^\infty
[2k\pi i-\log(z)]^{s-1}e^{2k\pi ai}](/2012-wikipedia_en_all_nopic_01_2012/I/b61c0d324fea149a7dd25650f5d278a9.png)
![\Phi(-z,s,a)=z^{-a}\Gamma(1-s)\sum_{k=-\infty}^\infty
[(2k%2B1)\pi i-\log(z)]^{s-1}e^{(2k%2B1)\pi ai}](/2012-wikipedia_en_all_nopic_01_2012/I/aa317267200481850e727bbb0d5c5462.png)